inf-428-data-analytics-online

Distributions and Confidence Intervals

Normal Distribution

• a.k.a. Guass, a.k.a. Bell Curve
• many measurements define the normal distribution
• defined by mean and standard deviation and calculated as follows

Generating Normal Distribution

see notebook

Confidence Interval

• Range of values defined so that there is a specified probability a value lies within it.
• ie 95% confidence interval is a range of values that we are 95% certain contains the value.
• Confidence interval can be calculated from mean and standard deviation of a distribution.

For example in Python the following code calculates the confidence interval of a single draw from a distribution with given mean and standard deviation

import numpy as np
import scipy
test = np.array([1,2,3,2,1,4]);
scipy.stats.norm.interval(0.95, test1.mean(), test1.std())

CONFIDENCE INTERVAL OF THE MEAN

• A mean calculated from sample data has an error itself
• Often we are interested in quantifying this error with a confidence interval
• In this case we need a statistic that estimates the deviation of the mean
• This is called standard error.

  Standard deviation vs standard error

• standard deviation measures how far datapoints are from average
  
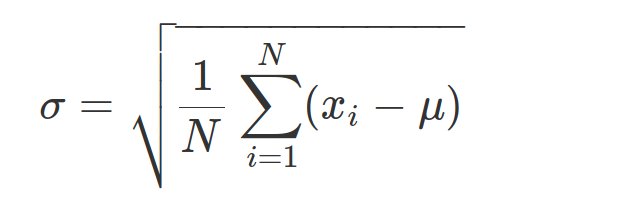
• standard error measures deviation of the mean
  

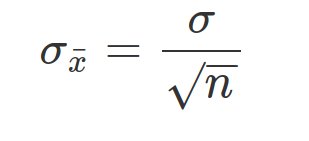
Confidence Interval of the Mean in Practice

• Range of values defined so that there is a specified probability the mean of the distribution lies within it.
• ie 95% confidence interval is a range of values that we are 95% certain contains the mean.
• Confidence interval can be calculated from mean and standard error of a distribution.

In Python

# in Python
import scipy
# assume a is an array
sample_mean=np.mean(a);
standard_error=scipy.stats.sem(a)

scipy.stats.t.interval(0.95, len(a)-1, loc=sample_mean, scale=standard_error)